1、引言
传感器是仪器仪表和测量系统的核心部件，是过程控制系统的首要环节，其设计的目标，是用户选择的依据。根据被测量是否随时间变化，传感器的性能指标分为静态和动态两大类。目前，国内外对传感器的静态特征研究较为深入和全面，而对动态特征研究较少。但随着科技的发展，人们愈来愈多地要求测量动态非电量或运动过程中测量非电量。例如航空、航天飞行器某些部件的瞬变温度、速度和压力的测量，要能迅速反映被控参量的变化，否则，整个控制系统就无法正常工作。传感器的动态品质将更引起人们的重视，提高传感器动态响应的快速性，可从两方面入手。一是改变其结构、参数和设计；二是进行动态补偿。本文正是针对磁电式传感器在相对测量方面具有广泛的运用前景，而硬件选型的计算及动态特性的研究相当复杂，设计了磁电式传感器材料选型的软件包程序，对其结构参数的磁电式传感器是利用电磁感应定律（e＝
－k将输入量转换成感应电势输出的一种传感器，也是建立在双向传感器的统一理论的基础上。这种传感器不需要辅助电源，所以是一种有源传感器，也称作感应式传感器或电动式传感器。2、磁电式传感器的主要元件的设计计算
磁电式传感器的硬件材料的设计包括磁路元件的设计、线圈的设计及工作点的确定。下面就磁路设计讲述硬件材料设计的方法。
磁路设计中包括复杂的计算：工作气隙磁导
总磁导及漏磁系数的计算（A=A1+A2+A3+A4+A5+A6）。设计时一般根据结构的大小初步确定磁路系统，根据磁路就可以计算磁感应强度，这样由技术指标给定的灵敏度值和已定磁感应强度值就可求得线圈导线总长度。如果气隙尺寸已定，线圈平均周长也就确定了，因此匝数可定。而如此复杂的计算，用人工去完成既费时又不准确，甚至会影响实际生产和科学实验，为此，本文设计了对磁电式传感器所有元件材料进行计算的软件包程序，并且各参数之间可以相互传递。例如漏磁导A6的计算软件界面如图1所示。
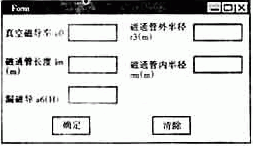
图1 漏磁导A6的计算
3、磁电式传感器动态特性的研究
磁电式传感器动态特性的研究包括相对测量的数学模型的推导、动态参数的计算及动态特性的输出。
3.1 相对测量的数学模型
设永久磁铁的质量（也称质量块）为m，弹簧刚度为K，阻尼器的阻尼系数为c，传感器的壳体与被测体刚性固定，线圈又与壳体刚性固定，所以当被测体运动时，传感器的壳体和线圈产生相同运动。
设x0为被测体（振动体）的绝对运动位移，xm为质量块（磁钢）的绝对运动位移，xt＝xm－x0为质量块与壳体（被测体）之间的相对运动位移。
取永磁体为隔离体，当被测体产生位移x0时，在它上面受到三个力的作用，当受力平衡时，有磁电式传感器动态特性的研究包括相对测量的数学模型的推导、动态参数的计算及动态特性的输出。
3.1 相对测量的数学模型
设永久磁铁的质量（也称质量块）为m，弹簧刚度为K，阻尼器的阻尼系数为c，传感器的壳体与被测体刚性固定，线圈又与壳体刚性固定，所以当被测体运动时，传感器的壳体和线圈产生相同运动。
设x0为被测体（振动体）的绝对运动位移，xm为质量块（磁钢）的绝对运动位移，xt＝xm－x0为质量块与壳体（被测体）之间的相对运动位移。
=0，则有：
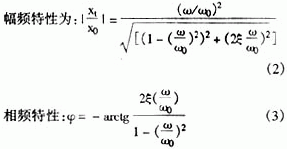
由式（1～2）可知：当ωω01时，xt＝x0。
这就是说，当被测体的振动频率ω比传感器的固有频率ω0大得很多时（通常ω≥3ω0）即可，质量块（磁钢）与被测体（线圈）之间的相对运动位移xt，就接近于被测体的绝对位移x0。此时可将质量块视为对一个静止坐标而言是静止不动的，这样就可以用测量线圈对质量块的相对运动来代替被测体（线圈）的绝对位移x0。这就是相对测量的基本原理。
3.2 动态参数的设计计算
动态参数的设计计算包括可动部分质量、弹簧刚度、阻尼系数等参数的设计计算。下面以可动部分质量的设计计算为例讲述其设计过程。
（1） 可动部分质量的设计计算
可动部分主要包括：顶杆、线圈的骨架、导线、线圈的质量。
导线：m1＝0．0181（克）；骨架：ρ＝2．7×103；v1＝лd（m3）；m2＝ρv1（克）；顶杆直径为D1，密度为ρ1，顶杆长为2，S＝JID21／4，m3＝ρ12S（克）；所以，总质量m＝m1＋m2＋m3（克），从而确定传感器的外壳材料。所有计算由VB编程完成，其具体分析见图2。
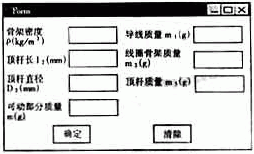
图2 可动部分质量的计算
3.3 动态特性的描述
由磁电式传感器的物理模型及其二端口网络理论可得，传感器的实际传递矩阵为：
从而由传感器输出端的电压和电流求得机械部分的参变量F及v。反之，由机械部分的F和v可求得电路部分的电压e和电流i。本文用VB编程实及相频特性输出曲线如图4、5。利用3．2节中传递过来的m、k、c等参数是3.2 节中传递过来的。其具体分析见图3.
描述传感器的方法除了参数模型的传递矩阵外，还可利用非参数模型的幅频特性分析。因此可利用幅频特性和相频特性来描述磁电式传感器的工作机理。根据（2）、（3）式数学模型编制了幅频特性及相频特性输出曲线如图4、5。利用3.2节中传递过来的m、k、c等参数及ξ值就可得到具体的幅频特性及相频特性输出曲线。
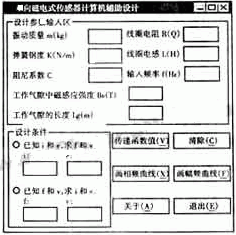
图3 机械部分和电路部分计算图
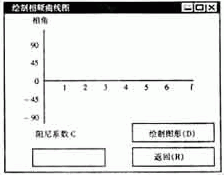
图4 相频特性曲线
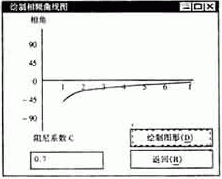
图5 相频特性曲线
4、磁电式传感器的误差分析及误差补偿
4.1 磁电式传感器的误差分析
磁电式传感器的误差主要有温度误差、永久磁铁的不稳定性误差、磁电式传感器的非线性误差。下面就温度误差产生的原因及补偿方法进行阐述。
温度误差
在磁电式传感器中，温度引起的误差是一个重要问题，必须加以计算。当测量电路输入电阻为Ri时，磁电式传感器的输出电流i0为：
4.1 磁电式传感器的误差分析
磁电式传感器的误差主要有温度误差、永久磁铁的不稳定性误差、磁电式传感器的非线性误差。下面就温度误差产生的原因及补偿方法进行阐述。
温度误差
在磁电式传感器中，温度引起的误差是一个重要问题，必须加以计算。当测量电路输入电阻为Ri时，磁电式传感器的输出电流i0为：
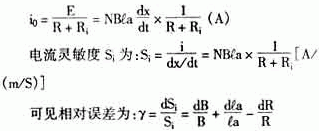
当温度变化时，上式中右侧的三项都不等于零。根据此数学模型，用VB编程对各项参数修改，维持传感器灵敏度为常数。
4.2 磁电式传感器的误差补偿
磁电式传感器在测量过程中由于受外界温度、压力、电磁场的影响及自身结构的限制，在实际操作中产生了各种误差，因此有必要设计新的传感器来代替旧的，或者就传感器本身改变其结构或参数，实验证明后一种方法比较可行，而且经济易实现。下面就二阶传感器的补偿方法及补偿效果加以阐述。
（1） 二阶模型的补偿环节
设传感器的二阶模型为：H（s）＝（b1s＋b2）／（s2＋a1s＋a2）
有两种方法构造补偿环节：第一种是将传感器的零极点全部消去，换上合适的极点，此时，补偿环节为：
磁电式传感器在测量过程中由于受外界温度、压力、电磁场的影响及自身结构的限制，在实际操作中产生了各种误差，因此有必要设计新的传感器来代替旧的，或者就传感器本身改变其结构或参数，实验证明后一种方法比较可行，而且经济易实现。下面就二阶传感器的补偿方法及补偿效果加以阐述。
（1） 二阶模型的补偿环节
设传感器的二阶模型为：H（s）＝（b1s＋b2）／（s2＋a1s＋a2）
有两种方法构造补偿环节：第一种是将传感器的零极点全部消去，换上合适的极点，此时，补偿环节为：
（2） 补偿步骤及仿真结果
采用零极点相消方法进行动态补偿的步骤为：
- 系统辨识法建模；
- 通过仿真，求出阶跃响应，判断动态性能是否符合要求；
- 不符合要求则求传感器模型的零极点；
- 确定动态补偿数字滤波器参数；
- 与传感器相连，得出新的等效系统；
- 等效系统与传感器阶跃响应的比较，判断补偿效果。
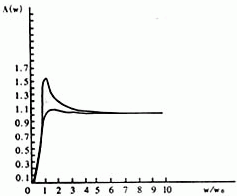
图6 零级点相消法仿真图
5、结论
磁电式传感器的计算机辅助设计具有很强的实用性和经济性，在原模型的基础上，参数稍加变动，既改善动态品质，又保持原系统的特点。零极点配置法设计补偿环节，仿真结果显示补偿效果非常明显。
